MATLABのFigureのX軸Y軸をX→Y、Y→X逆にする方法

　MATLABで書いたFigure(グラフなど)のX軸Y軸をX→Y、Y→Xと逆にしたい場合があります。plot(x,y)のような関数なら、plot(y,x)に変更すれば、可能ですが、hist(ヒストグラム),imview(イメージビューワ内にイメージを表示)などには、適用できません(?)。この場合は、view(90,90)の関数をすると便利だと思います。

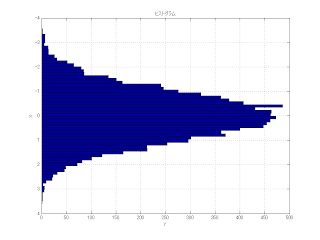
%----------------- MATLABソース -----------------%
y = randn(10000,1);
hist(y,60); %ヒストグラム
title('ヒストグラム');
xlabel('X');
ylabel('Y');
grid on;
%3次元グラフの視点の指定
view(90,90); % AZ=90, EL=90
%----------------- MATLABソース -----------------%

実行の結果

2つの色の違うボールのアニメーション

%----------------- MATLABソース -----------------%
for t=0:0.02:4*pi;
   x=sin(t)*10;
   y=cos(t)*10;
   plot(t,x,'.b',t,y,'.k','MarkerSize',30);
   xlim([0 2*pi]);
   ylim([-10 10]);
   grid on;
   % 描画を強制更新
   drawnow
end
%----------------- MATLABソース -----------------%

MATLABのLAPACE関数の利用方法

L = LAPLACE(F) は、デフォルトの独立変数 t をもつスカラシンボリックオブジェクトF のラプラス変換です。

%----------------- MATLABソース -----------------%
syms t s a;
f= {
  t^4 ;
  1/sqrt(s) ;
  exp(-a*t) ;
  };
N = length(f);
for i=1:N
  L = laplace(f{i}); %ラプラス変換
  disp(f{i});
  disp('ラプラス変換後');
  disp(L);
  disp('----------------------------------');
end
%----------------- MATLABソース -----------------%

実行の結果

t^4
ラプラス変換後
24/s^5
----------------------------------
1/s^(1/2)
ラプラス変換後
(pi/t)^(1/2)
----------------------------------
exp(-a*t)
ラプラス変換後
1/(s+a)
----------------------------------

MATLABのIFOURIER関数の利用方法

f = IFOURIER(F)は、デフォルトの独立変数 w をスカラシンボル F の逆フーリエ変換です。

%----------------- MATLABソース -----------------%
syms w
F = {
   exp(-abs(w)) ;
   2*exp(-abs(w))-1 ;
   };
N = length(F);
for i=1:N
   f = ifourier(F{i}); %逆フーリエ積分変換
   disp(F{i});
   disp('逆フーリエ積分変換');
   disp(simple(f));
   disp('----------------------------------');
end
%----------------- MATLABソース -----------------%
実行の結果
exp(-abs(w))
逆フーリエ積分変換
1/(1+x^2)/pi
----------------------------------
2*exp(-abs(w))-1
逆フーリエ積分変換
-dirac(x)+2/(1+x^2)/pi
----------------------------------

MATLABのFOURIER関数の利用方法

　F = FOURIER(f) は、デフォルトの独立変数 x をもつシンボリックスカラf のフーリエ変換です。デフォルトでは、w の関数を出力します。

%----------------- MATLABソース -----------------%
syms x v;
f= {
exp(-x^2) ;
exp(-abs(x)) ;
x*exp(-abs(x)) ;
sin(x)*exp(-x^2) ;
};
N = length(f);
for i=1:N
F = fourier(f{i}); %フーリエ積分変換
disp(f{i});
disp('フーリエ積分変換後');
disp(F);
disp('----------------------------------');
end
%----------------- MATLABソース -----------------%

実行の結果

exp(-x^2)
フーリエ積分変換後
pi^(1/2)*exp(-1/4*w^2)
----------------------------------
exp(-abs(x))
フーリエ積分変換後
2/(1+w^2)
----------------------------------
x*exp(-abs(x))
フーリエ積分変換後
-4*i/(1+w^2)^2*w
----------------------------------
sin(x)*exp(-x^2)
フーリエ積分変換後
-i*pi^(1/2)*sinh(1/2*w)*exp(-1/4*w^2-1/4)
----------------------------------

MATLABのGPLOT関数の利用方法

GPLOT関数は、隣接行列を使ってノード集合(ネットワーク図)をプロットします。

%----------------- MATLABソース -----------------%
r = 1;
c = 2;
A = [
  %1 2 3 4
   0 1 0 1; % 1 ノード1は、ノード2,3に隣接ため、1
   1 0 1 0; % 2 ノード2は、ノード1,3に隣接ため、1
   0 1 0 1; % 3 ノード3は、ノード2,4に隣接ため、1
   1 0 1 0  % 4 ノード4は、ノード1,3に隣接ため、1
   ];
xy = [
   1 3; % ノード1の座標
   2 1; % ノード2の座標
   3 3; % ノード3の座標
   2 5  % ノード4の座標
   ];
subplot(r,c,1);
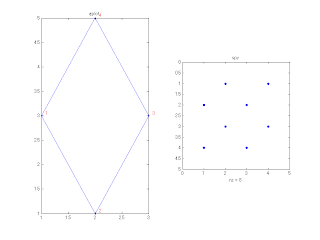
gplot(A,xy,'.--');
text(xy(:,1)+0.1,xy(:,2)+0.05,('1234')', 'HorizontalAlignment','center','color','red');
title('gplot');

subplot(r,c,2);
spy(A); %行列 S のスパースパターンをプロットします。
title('spy');
print('-dpng','-r100','gplot.png');
%----------------- MATLABソース -----------------%

実行の結果

マンデルブロ集合とマンデルブロ図形

マンデルブロ集合とは、ある複素数Cに対して，次のような漸化式を計算します．mが無限に大きくなっても |z(m)|^2 が発散しないような複素数Cの集合をマンデルブロ集合と呼びます。
　Z(0) = 0.0
　Z(m+1) = Z(m)*Z(m) + C
マンデルブロ図形とは複素平面上に描かれるフラクタル図形(自己相似図形)の一種で、元IBMの研究者であったBenoit Mandelbrotによって発見されました。自己相似図形とは自分自身の定義を自分自身で行っている、つまり細部の構造・形状が全体の構造・形状と同一であるような図形のことです。マンデルブロー図形をズーミングすると、全体の形状と同一の形状が細部に集まって全体を構成しています。

%----------------- MATLABソース -----------------%
n=60;
m=1000;
Z=zeros(m); %m行m列の零の行列の作成
C=X+i*Y;
for k=1:n;
 Z=Z.^2+C;
 W=exp(-abs(Z));
end
colormap jet(256); %カラールックアップテーブル
pcolor(W); %擬似カラー(チェッカーボード)プロット
shading flat; %カラーシェーディングモード
axis('square','equal','off');
print('-dpng','-r200','mandel.png');
%----------------- MATLABソース -----------------%

実行の結果

MATLABのFFT関数の利用方法

　高速フーリエ変換（Fast Fourier Transform, FFT）とは、離散フーリエ変換 (Discrete Fourier Transform, DFT) を計算機上で高速に計算するアルゴリズムです。
　ここで、FFTを使って、太陽黒点の周期の算出する例題を紹介します。
　太陽の黒点活動について、1700 年～1987 年までの間、1 年毎に観測したWolfer 数データが、sunspot.dat にあります。黒点の動きは、太陽黒点の活動は、約11年毎に最大になる周期をもっていることが知られていますが、フーリエ変換を用いて、黒点の動きの近似周期を求めます。

%----------------- MATLABのソース -----------------%
%---  この例題はMATLABのデモに参考したものです。---%
r = 2;
c = 2;
%過去300年にわたって太陽の黒点活動
load sunspot.dat;
year = sunspot(:,1);
wolfer = sunspot(:,2);

subplot(r,c,1);
plot(year,wolfer);
grid on;
title('太陽の黒点活動')
xlabel('年');ylabel('Wolfer数');

Y = fft(wolfer); %離散フーリエ変換
N = length(Y);
Y(1) = [];
power = abs(Y(1:N/2)).^2;
nyquist = 1/2;
freq = (1:N/2)/(N/2)*nyquist;
subplot(r,c,2);
plot(freq,power), grid on
xlabel('周期/年数')
title('ピリオドグラム')

period = 1./freq;
subplot(r,c,3);
plot(period,power), axis([0 40 0 2e7]), grid on
ylabel('パワー');
xlabel('年数/周期')

[mp,index] = max(power);
period(index)
print('-dpng','-r100','fft_sunspot.png');
%----------------- MATLABのソース -----------------%

実行の結果

candle関数(キャンドルスティックチャート)の利用方法

　candle関数(キャンドルスティックチャート)の利用方法を紹介します。 candle関数は有価証券(株、為替のレートなど)の価格の高値 HIGH、安値 LOW、終値 CLOSE、始値 OPEN のデータが与えられた時に、キャンドルスティックチャートをプロットします。

%----------------- MATLABのソース -----------------%
% 2007/11/01～2007/11/19のドル・円レートデータ
usdjpy = {
%     日付     始値    高値    安値    終値
'2007/11/01' 115.44  115.92  114.48  114.67
'2007/11/02' 114.67  115.46  114.38  114.85
'2007/11/05' 114.78  114.82  114.02  114.54
'2007/11/06' 114.54  114.78  114.28  114.72
'2007/11/07' 114.72  114.76  112.63  112.64
'2007/11/08' 112.64  113.37  112.25  112.67
'2007/11/09' 112.67  112.87  110.50  110.70
'2007/11/12' 110.28  110.79  109.14  109.43
'2007/11/13' 109.43  111.00  109.43  110.92
'2007/11/14' 110.92  111.75  110.76  111.32
'2007/11/15' 111.32  111.68  110.23  110.30
'2007/11/16' 110.30  111.35  109.78  111.09
'2007/11/19' 110.88  111.07  109.77  109.81
};

ymd  = datenum(strvcat(usdjpy{:,1}),'yyyy/mm/dd');
open = [usdjpy{:,2}]';
high = [usdjpy{:,3}]';
low  = [usdjpy{:,4}]';
clos = [usdjpy{:,5}]';
%時系列オブジェクトの取り込む
data = fints(ymd,[open high low clos],{'OPEN','HIGH','LOW','CLOSE'});
candle(data); %キャンドルスティックチャート
axis tight
%日付を書式化した目盛りのラベルを付ける
datetick('x','mm/dd');
title('ドル・円のチャート'); xlabel('日付'); ylabel('レート');
grid on;
print('-dpng','-r100','usdjpy_chart.png');
%----------------- MATLABのソース -----------------%

実行の結果

MATLAB内からのPostgreSQLクエリーの直接実行

Database Toolboxの利用により、データベースに保管されている情報をMATLABのデータ解析および可視化ツールを用いて分析することが可能です。MATLAB環境内の操作において、SQLを使って、データベースからの読み込みやデータの書き出し、データベースクエリーに対するシンプルまたは高度な条件設定を行うことができます。
ここで、MATLAB環境内からPostgreSQLサーバへのアクセス方法を紹介します。

%----------------- MATLABのソース -----------------%
dbname = ''; %データベース名
user = ''; %ユーザ名
pwd = ''; %パスワード
db = struct('dbname',dbname,'user',user,'pwd',pwd);
%指定したPostgeSQLデータベースへ、ユーザ名とパスワードを入力してアクセスします。
connect = database(db.dbname, db.user, db.pwd, 'org.postgresql.Driver', 'jdbc:postgresql://localhost:5432/');
sql = 'select * from usdjpy';
%データを選択するため、カーソルをオープンし、SQLクエリーを発行します。
curs = exec(connect,sql);
%setdbprefs('DataReturnFormat','cellarray');
setdbprefs('DataReturnFormat','structure');
data = fetch(curs);
close(curs);
%----------------- MATLABのソース -----------------%

レスラーアトラクタ

レスラーモデルに参考
　レスラーモデルとは、チュービンゲン大学のレスラー(O.E.Rossler)によって提案されたストレンジアトラクタで、非線形項のみを含む非線形微分方程式である。

%-----------------  MATLABのソース  -----------------%
%----------------- main_rossler.m  -----------------%
function main_rossler
r = 2;
c = 2;
[t,xyz] = ode45('rossler',[0,500],[4;0;0]);
x = xyz(:,1); xmin = min(x); xmax = max(x);
y = xyz(:,2); ymin = min(y); ymax = max(y);
z = xyz(:,3); zmin = min(z); zmax = max(z);

aviobj = avifile('rossler.avi');

for i=1:length(t)
subplot(r,c,1);
plot3(x(1:i),y(1:i),z(1:i),...
   x(1),y(1),z(1),'or',...
   x(i),y(i),z(i),'ob');
axis([xmin xmax ymin ymax zmin zmax]);
xlabel('x'); ylabel('y'); zlabel('z');

subplot(r,c,2);
plot(x(1:i),y(1:i),...
   x(1),y(1),'or',...
   x(i),y(i),'ob');
axis([xmin xmax ymin ymax]);
xlabel('x'); ylabel('y');

subplot(r,c,3);
plot(x(1:i),z(1:i),...
   x(1),z(1),'or',...
   x(i),z(i),'ob');
axis([xmin xmax zmin zmax]);
xlabel('x'); ylabel('z');

subplot(r,c,4);
plot(y(1:i),z(1:i),...
   y(1),z(1),'or',...
   y(i),z(i),'ob');
axis([ymin ymax zmin zmax]);
xlabel('y'); ylabel('z');

%pause(0.01);
%F(i) = getframe(GCF);
F = getframe(GCF);
aviobj = addframe(aviobj,F);
end
aviobj = close(aviobj);
%movie2avi(F,'rossler.avi');
end
%----------------- main_rossler.m  -----------------%

%----------------- rossler.m -----------------%
function xyz = rossler(t,y)
a = 0.2;
b = 0.2;
c = 6.0;
xyz = [ -y(2) - y(3)
       y(1) + a*y(2)
       b + y(1)*y(3) - c*y(3) ];
end
%----------------- rossler.m -----------------%
%----------------- MATLABのソース -----------------%

実行の結果

ローレンツ・アトラクタ

ローレンツモデルに参考

　ローレンツモデルとは、気象学者エドワード・ローレンツ (Edward N. Lorenz)は1963年に "Deterministic nonperiodic flow"というカオスの研究上重要な位置を占めるにことになる論文を発表した。
　このモデルは、上下に温度差のある流体の運動差によって、対流から乱流へ転移してく運動を記述するモデルである。一般的な対流の運動方程式、連続の方程式、熱伝導の方程式を用いて導かれる。

%-----------------  MATLABソース  -----------------%
%----------------- lorenz_main.m  -----------------%
function main
r = 2;
c = 2;
[t,xyz] = ode45('lorenz',[0,30],[5;3;1]);
x = xyz(:,1); xmin = min(x); xmax = max(x);
y = xyz(:,2); ymin = min(y); ymax = max(y);
z = xyz(:,3); zmin = min(z); zmax = max(z);

for i=1:length(t)
   subplot(r,c,1);
   plot3(x(1:i),y(1:i),z(1:i),...
       x(1),y(1),z(1),'or',...
       x(i),y(i),z(i),'ob');
   axis([xmin xmax ymin ymax zmin zmax]);
   xlabel('x'); ylabel('y'); zlabel('z');
  
   subplot(r,c,2);
   plot(x(1:i),y(1:i),...
       x(1),y(1),'or',...
       x(i),y(i),'ob');
   axis([xmin xmax ymin ymax]);
   xlabel('x'); ylabel('y');
  
   subplot(r,c,3);
   plot(x(1:i),z(1:i),...
       x(1),z(1),'or',...
       x(i),z(i),'ob');
   axis([xmin xmax zmin zmax]);
   xlabel('x'); ylabel('z');
  
   subplot(r,c,4);
   plot(y(1:i),z(1:i),...
       y(1),z(1),'or',...
       y(i),z(i),'ob');
   axis([ymin ymax zmin zmax]);
   xlabel('y'); ylabel('z');
  
   pause(0.01);
   F(i) = getframe(GCF);
end
movie2avi(F,'lorenz.avi');
end
%----------------- lorenz_main.m  -----------------%

%-----------------    lorenz.m    -----------------%
function xyz = lorenz(t,y)
   s = 10;
   b = 8/3;
   r = 28;
   xyz = [ -s .* y(1) + s .* y(2)
            r .* y(1) - y(2) - y(1) .* y(3)
            y(1) .* y(2) - b .* y(3) ];
end
%-----------------    lorenz.m    -----------------%
%-----------------  MATLABソース  -----------------%

実行の結果

ブラウン運動

ブラウン運動とは、1827年、ロバート・ブラウンが、花粉が水の浸透圧で破裂し水中に流失し浮遊した微粒子を顕微鏡下で観察中に発見した現象。液体中のような媒質中（媒質としては気体、固体もあり得る）に浮遊する微粒子が、不規則（ランダム）に運動する現象である。

長い間原因が不明のままであったが、1905年、アインシュタインにより、熱運動する媒質の分子の不規則な衝突によって引き起こされる現象であるとして説明する理論が発表された。

２次元ランダムウォークの軌跡。ステップを小さくした極限ではブラウン運動が得られる。

%----------------- MATLABソース -----------------%
function main()
N = 128*16;
cx = 0.2; cy = 0.2;
sx = 0; sy = 0;
x(1) = 0; y(1) = 0;

for i=2:N
    [dx dy] = randwalk;
    sx = sx + cx * dx;
    sy = sy + cx * dy;
    x(i) = sx;
    y(i) = sy;
end
minx = min(x); maxx = max(x);
miny = min(y); maxy = max(y);
for i=1:N-1
    plot(x(1:i),y(1:i),'k',x(i),y(i),'o',x(1),y(1),'or');
    axis equal;
    axis([minx maxx miny maxy]);
    pause(0.01)
    F(i) = getframe;
end
movie2avi(F,'brownian.avi');
end

function [dx dy] = randwalk
dx = rand(1)-0.5;
dy = rand(1)-0.5;
end
%----------------- MATLABソース -----------------%

実行の結果

ランダムウォーク

　ランダムウォークとは、「次に現れるものの確率」が不規則（ランダム）に決定される運動のこと。一見すると、「不規則で落ち着きのない動き」をしているように見えても、全体的に見ると実は「連続である」ことを指す。

%----------------- MATLABソース -----------------%
function main()
N = 128*16;
cx = 0.1; cy = 0.1;
sx = 0; sy = 0;
x(1) = 0; y(1) = 0;
for i=2:N
    [dx dy] = randwalk;
    sx = sx + cx * dx;
    sy = sy + cx * dy;
    x(i) = sx;
    y(i) = sy;
end

minx = min(x); maxx = max(x);
miny = min(y); maxy = max(y);
for i=1:N-1
    plot(x(1:i),y(1:i),'k',x(i),y(i),'o',x(1),y(1),'or');
    axis equal;
    axis([minx maxx miny maxy]);
    pause(0.01)
    F(i) = getframe;
end
movie2avi(F,'randomwalk.avi');
end

function [dx dy] = randwalk
w=0;
while w==0
    w=rand(1)-0.5;
    w = sign(w);
end
dx = 0; dy = 0;
if ceil(2*rand(1)) == 1
    dx = w;
else
    dy = w;
end
end
%----------------- MATLABソース -----------------%

実行の結果

正規確率密度と正規累積分布

%----------------- MATLABソース -----------------%
mx = 3;
dx = 0.1;
r = 2;
c = 1;
x = -mx:dx:mx;
mu = 0; %平均値
sigma = 1; %標準偏差
%正規確率密度関数
f = normpdf(x,mu,sigma);
%正規累積分布関数
F = normcdf(x,mu,sigma);
subplot(r,c,1);
plot(x,f);
title('標準正規確率密度');
grid on;
subplot(r,c,2);
plot(x,F);
title('標準正規累積分布');
grid on;
print('-dpng','-r100','normpdf.png');
%----------------- MATLABソース -----------------%

出力結果

ボロノイ図(Voronoi diagram)

　平面上に配置された点群において，各点の勢力圏に応じて平面を分割した図が，二次元のボロノイ図(Voronoi diagram)です。

%---------------- MATLABソース　----------------%
N = 256;
S = 4;
x = rand(N,1)*S; % 点x
y = rand(N,1)*S; % 点y
%Voronoi線図
voronoi(x,y);
print('-dpng','voronoi.png');
%---------------- MATLABソース　----------------%

MATLABによるボロノイ図

peaks 関数のアニメーション

%--------Matlabのソース--------
%PEAKSは、ガウス分布の変換とスケーリングによって得られる2変数関数
Z = peaks;
surf(Z);
%ムービーフレームのメモリの初期化
M = moviein(60);
axis manual
set(gca,'nextplot','replacechildren');
for j = 1:60
surf(sin(2*pi*j/20)*Z,Z)
%ムービーフレームの取り出し
M(:,j) = getframe;
end
% ムービーからAVIムービーを作成
movie2avi(M,'peaks.avi')
%--------Matlabのソース--------

アニメーションの結果

よく利用されるMATLABのシンボリック

SYM シンボリックな数値、変数、オブジェクトの作成
例: sym('x') sym(1/3,'r')
SYMS シンボリックオブジェクト作成のショートカット
例: syms x y z
VPA 可変精度の演算
例：vpa(pi,128)
DOUBLE 倍精度に変換
例: double(x)
CHAR キャラクタ配列(文字列)の作成
例: char(x)
FINDSYM シンボリック式、または、行列内の変数の検出
例: syms x y z, z=x^2+y^2, findsym(z) は、x,yを出力する
FINVERSE 逆関数
finverse(f)
SYMSUM シンボリックな総和
SYMSUM(S, v) は、v について無限大の総和を求めます。
SYMSUM(S, a, b) と SYMSUM(S, v, a, b)は、a から b までのシンボリック式
の総和を求めます。
SOLVE 代数方程式のシンボリックな解
例: solve('x^2-1=0')
CLASS オブジェクトの作成、または、オブジェクトのクラスの出力
例: class(obj)
SUBEXPR 共通する部分式による式の書き換え
SIMPLE シンボリック式、または、行列の最も短い表現の検索
PRETTY シンボリック式のプリティプリント
LATEX シンボリック式の LaTeX 表現
PRIMES 素数のリストの作成
EXPAND シンボリックな展開
COLLECT 係数をまとめます。
NUMDEN シンボリック式の分子と分母
SUBS シンボリックな代入
COMPOSE 関数の合成,COMPOSE(f,g)は、f(g(y))を出力します
DIFF 微分
DIFF(S) は、FINDSYMで決定されるような自由変数に関して、シンボリック式 S
を微分します。
INT 積分
INT(S) は、FINDSYM で定義されるようなシンボリック変数について、S の
不定積分を出力します。
DSOLVE 常微分方程式のシンボリックな解
例: x = dsolve('Dx = -a*x','x(0) = 1','s') は、つぎの結果を出力します。
x = exp(-a*s)
TAYLOR Taylor 級数展開
TAYLOR(f) は、f に対して5次の Maclaurin 多項式近似を出力します。
3つのパラメータを任意の順序で与えることができます。
例: taylor(sin(x),pi/2,6) は、1-1/2*(x-1/2*pi)^2+1/24*(x-1/2*pi)^4 を
出力します。
DET シンボリックな行列式
DET(A)は、シンボリック行列Aの行列式です。
DIRAC Delta関数
HEAVISIDE Step関数
FOURIER フーリエ積分変換
IFOURIER 逆フーリエ積分変換
LAPLACE ラプラス変換
ILAPLACE 逆ラプラス変換